Stockage de l'électricité par pompage turbinage thermique
Sans une bonne batterie, les énergies renouvelables ne seront jamais crédibles. Malheureusement, il n'existe actuellement aucune bonne solution de stockage de l'électricité : soit que c'est trop cher, ou la conservation de l'énergie est limitée dans le temps, la fabrication est trop polluante ou bien on perd les trois quarts de ce qu'on a stocké comme avec l'hydrogène et c'est encore pire avec les carburants de synthèse. Sans une bonne batterie, nos investissements dans les éoliennes n'auront eu aucun sens. C'est pourquoi j'aimerais vous présenter une batterie qui semble promise à un bel avenir et qui fonctionne suivant le principe du pompage turbinage thermique. Ce stockage a été breveté en 1929 par Marguerre. Cependant, il est méconnu de nos jours, alors qu'il est le complément indispensable des énergies renouvelables. Voici de quoi il s'agit.
Vous connaissez le pompage turbinage par gravité, les STEP : on pompe l'eau d'un lac inférieur dans un lac supérieur lors du stockage, et pour récupérer l'électricité, on fait redescendre l'eau au travers d'une turbine hydraulique. Le pompage turbinage thermique est similaire, mais au lieu de pomper de l'eau, on pompe des calories avec une pompe à chaleur en créant un réservoir très froid et un réservoir très chaud. Pour récupérer l'électricité, cette différence de températures est appliquée à une turbine à vapeur. L'avantage est que les dimensions des réservoirs sont beaucoup plus réduites que celles d'un lac et qu'il n'est pas nécessaire d'avoir un site au relief bien particulier. Cela vient du fait que beaucoup plus d'énergie peut être stockée dans la chaleur que dans les masses. Faisons un petite comparaison : prenons un mètre cube d'eau et chauffons-le de 15 °C à 95 °C d'une part et d'autre part une grue soulève ce mètre cube (qui pèse une tonne) à une hauteur de 100 mètres. Dans ces conditions, on a stocké 341 fois plus d'énergie dans la chaleur que dans les masses. Nous voyons donc qu'il faut privilégier le thermique.
Cette batterie qui est nécessairement stationnaire peut donc être installée dans les PME possédant de nombreux panneaux solaires. L'efficacité aller-retour de cette batterie, c'est-à-dire ce qu'on peut retirer de ce qu'on a stocké, se situe entre 50 % et 60 %, ce qui est mieux que les 25 % de l'hydrogène.
Cette batterie, qu'on peut également appeler batterie de Carnot avec pompe à chaleur, est composée de 4 éléments : un réservoir chaud, un réservoir froid, une pompe à chaleur et une turbine à vapeur.
La pompe à chaleur extrait les calories d'un réservoir qui devient très froid, y ajoute l'énergie à stocker qui vient des panneaux photovoltaïques ou des éoliennes et place le tout dans un réservoir qui devient très chaud. On a donc stocké l'électricité sous forme de chaleur. Pour récupérer l'électricité, cette différence de température est appliquée à une turbine à vapeur.
Prenons un exemple.
De nombreuses fermes ont 400 m² de panneaux photovoltaïques sur le toit de leurs hangars. En Belgique, ils produisent 400 kWh par jour en été. Si cette énergie est stockée dans une batterie dont l'efficacité aller-retour est 50 %, la capacité de stockage de cette batterie est de 200 kWh par jour. Si cette électricité est écoulée en 10 heures, cela signifie que la puissance de la turbine est de 20 kW. Cela pourrait être produit par les micro-turbines d'Enogia https://enogia.com/orc/ . Actuellement, ces micro-turbines fonctionnent à basse température (entre 70 °C et 120 °C) mais elles ne permettraient d'obtenir que 20 % d'efficacité aller-retour tandis que si ces micro-turbines fonctionnaient à 500 °C, cette efficacité se situe entre 50 % et 60 %.
La température dans le réservoir chaud va évoluer entre 500 °C et 300 °C. Cette température de 500 °C doit être atteinte grâce à la pompe à chaleur. Cela existe et je trouve cela épatant. La température moyenne dans le réservoir chaud est donc 400 °C. Le réservoir froid contiendra de l'eau qui est constamment en train de congeler et de décongeler. Ce réservoir contient donc un mélange d'eau liquide et de glace en proportions variables suivant les calories qui auront été extraites. Ce réservoir est donc toujours à 0°C.
Si nous appliquons ces températures de 400 °C et 0 °C à une turbine à vapeur, on peut calculer son rendement de Carnot, un rendement théorique qu'il n'est pas possible de dépasser. Ce rendement est dépendant uniquement des températures et il vaut (400 - 0) / (400 + 273) = 59,4 %. Nous avons ajouté 273 ° aux 400 °C pour obtenir les températures en degrés Kelvin.
Dans notre exemple, la batterie doit fournir 200 kWh, ce qui correspond aux 59,4 % utiles. Le réservoir froid doit refroidir la turbine en lui enlevant 100 % - 59,4 % = 40,6 % de l'énergie apportée à la turbine. Le réservoir froid devra donc contenir 40,6 / 59,4 * 200 kWh = 137 kWh. De façon théorique, le réservoir chaud devra apporter à la turbine 137 + 200 = 337 kWh.
Malheureusement, ceci serait exact si la transformation de l'énergie thermique en énergie mécanique était parfaite. Or, quand la vapeur frappe les aubes de la turbine, il y a des turbulences qui provoquent des pertes. Supposons que celles-ci s'élèvent à 20 %. On dira alors que la turbine a un rendement isentropique de 80 %. Cette perte doit permettre d'obtenir en sortie de la turbine 200 kWh consommés + le froid retiré au condenseur de la turbine, soit 137 kWh. Il faudra donc fournir à la turbine 337 kWh / 0,80 = 421 kWh. La perte isentropique vaut donc 421 - 337 = 84 kWh.
La perte dans le compresseur étant immédiatement dissipée au moment où l'énergie à stocker entre dans la batterie, elle ne doit donc pas être stockée et ne sera donc pas fournie à la turbine.
Supposons que le rendement isentropique du compresseur de la pompe à chaleur est également de 80 %. Le compresseur reçoit les calories du réservoir froid (137 kWh) et y ajoute l'énergie à stocker qui vient des panneaux solaires (200 kWh), sans oublier la perte isentropique dans la turbine qui subira elle-même une perte dans le compresseur. Cette perte majorée sera donc de 84 kWh / 0,8 = 105 kWh. Les panneaux solaires devront donc fournir à la batterie l'énergie à stocker soit 200 kWh ainsi que les pertes dans la turbine (84 kWh) et la perte dans le compresseur de la pompe à chaleur (105 kWh) qui sera directement dissipée, soit au total 200 kWh + 84 kWh + 105 kWh = 389 kWh. L'efficacité aller-retour de notre batterie sera 200 kWh / 389 kWh = 51,4 %, ce qui est mieux que les 25 % de l'hydrogène. La chaleur qui est retirée au condenseur de la turbine ne quitte pas la batterie et ne doit donc pas être apportée de l'extérieur.
Le réservoir froid sera fait en béton et contiendra de l'eau de pluie, car cette eau ne peut contenir de chlorures ou de sulfates qui attaquent le béton. Son volume sera de 137 kWh / 93 kWh/m³ nécessaires pour congeler 1 m³ d'eau, soit un réservoir froid de 1,5 m³. Le réservoir chaud contiendra un lit de roche, comme le basalte par exemple, ou des sels fondus. Les dimensions du réservoir chaud contenant du basalte seront données par
421 kWh / (500 °C - 300 °C) / 2.800 kg/m³ poids spécifique du basalte / 0,2 chaleur massique basalte * 860 kcal/kWh = 3 m³. Cependant, calculons quelle seront les déperditions de chaleur au travers des parois du réservoir chaud. Si c'est un cube de 1,5 m de côté, soit 3 m³, sa surface extérieure sera de 1,5 m * 1,5 m * 6 = 13,5 m².
Pour connaître les déperditions au travers des parois, j'utilise la formule : Surface * différence de température / épaisseur de l'isolant * coefficient de l'isolant * durée, soit après 15 jours de conservation :
13.5 m² * 400 °C / 2 m isolant * 0,04 coefficient laine de roche * 15 jours * 24 heures / 860 kcal/kWh = 45 kWh, alors que la contenance est de 421 kWh se trouvent dans le réservoir chaud, soit une perte de 22,6 % en 15 jours.
Un petit dessin vaut mieux qu'un long discours :
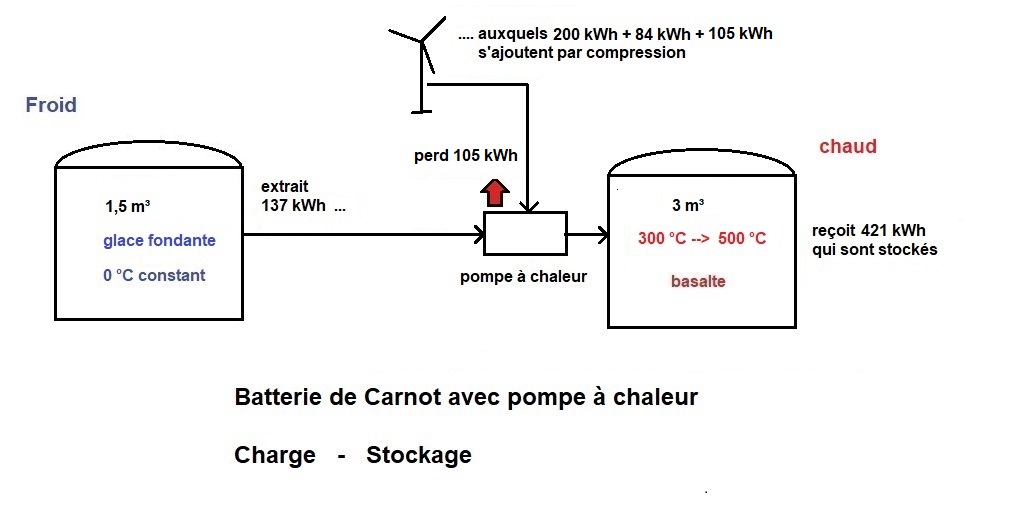
==================================================================
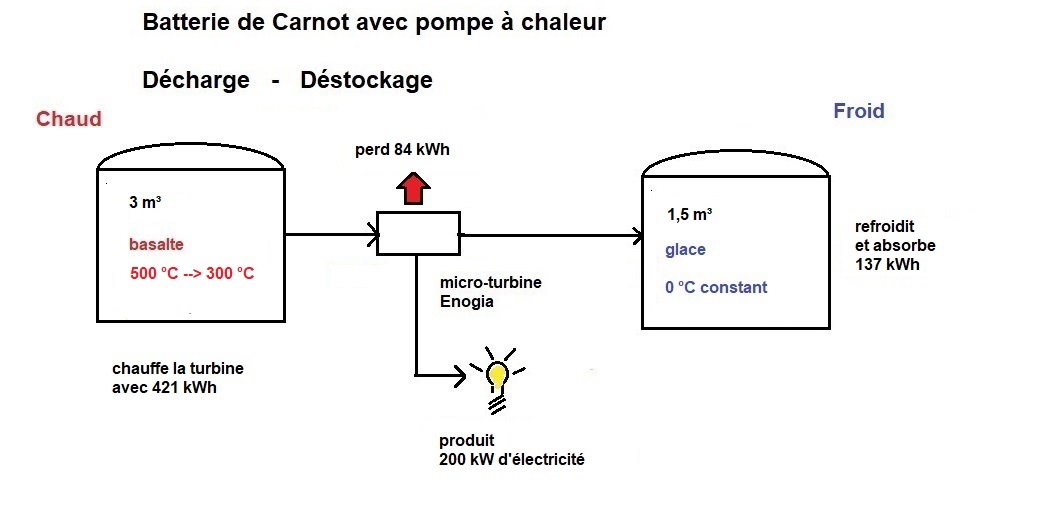
Si le réservoir chaud est plus grand, par exemple s'il contient 4.000 kWh, ce même calcul donnerait un réservoir qui sera un cube de 64 m³ avec 4 m de côté et la déperdition en 15 jours serait de 4 %. On voit donc que plus le réservoir est grand, au moins il perd de chaleur par rapport à ce qu'il contient.
Les énergies renouvelables sont diffuses. On peut donc les capter partout, et décentraliser les récepteurs pour utiliser leur électricité sur place est tout à fait logique. Pour reprendre l'exemple cité plus haut, 400 m² de panneaux solaires devraient être couplé à une batterie de 200 kWh. Si cette batterie est remplie et vidée chaque jour, et qu'elle doit fournir de l'électricité pendant 10 heures par jour, cela signifie que la puissance de la turbine doit être de 20 kW. C'est exactement ce que fait actuellement Enogia, mais à des températures comprises côté chaud entre 70 °C et 120 °C, car utilisées pour récupérer la chaleur fatale. J'attends avec impatience ces mêmes micro-turbines fonctionnant à 400 °C.
Cette batterie serait vraiment une avancée significative en vue de rendre les énergies renouvelables crédibles, car elle est constituée d'acier, de roches ou des sels fondus et d'eau, tous des éléments abondants dans la nature (il y a 2.000 fois plus de fer que de lithium dans le monde) et on n'est pas obligé d'assoiffer des régions entières comme on le fait avec le lithium.
Batterie de Carnot avec réservoirs à basse température.
Avec des températures inférieures à 120 °C dans le réservoir chaud , les batteries de Carnot avec pompe à chaleur ont une efficacité aller-retour de 20 %, alors qu'à 500 °C, elle est d'environ 60 %. Je me suis donc demandé comment les rendre performantes avec des basses températures dans les réservoirs. En effet, les installations avec des réservoirs à 500 °C doivent être réservées à l'industrie. Nous ne recevrons jamais les autorisations nécessaires pour les installer au contact du grand public ou chez des particuliers.
Mon idée consiste à équiper ce pompage turbinage thermique d'une turbine à vapeur d'eau à 500 °C où cette température n'est atteinte que juste avant l'entrée de la turbine, et rien qu'à cet endroit. La batterie se composera donc pour la décharge de la batterie d'un réservoir chaud contenant de l'eau dont la température varie de 95 °C à 50 °C, d'un réservoir froid contenant de la glace qui fond en partie, donc toujours à 0 °C, et d'un chauffage de la vapeur sèche à l'entrée de la turbine avec une résistance électrique qui reçoit une petite partie de l'électricité produite par la turbine et son alternateur. Au sortir du condenseur, nous aurons de l'eau liquide à 20 °C environ. Elle se vaporise ensuite complètement à une température légèrement plus élevée pour devenir de la vapeur sèche par le seul apport des calories fournies par le réservoir chaud entre 95 et 50 °C. Ensuite, une part de l'électricité produite par la turbine va servir à porter cette vapeur sèche de 95 °C à 500 °C.
Le rendement de Carnot, donc purement théorique et qui est le maximum qu'on peut idéalement atteindre est de (500 - 0) / (500 + 273) = 65 %.
La chaleur de vaporisation de l'eau à 20 °C est d'environ 600 kcal/kg eau.
Pour qu'un kg de vapeur sèche augmente d'un degré, il faut lui apporter 0,5 kcal. Entre 20 °C et 500 °C, il y a une différence de 480 °C, et 480 °C * 0,5 kcal/kg.°C = 240 kcal/kg qui seront fournis par l'électricité prélevée en sortie.
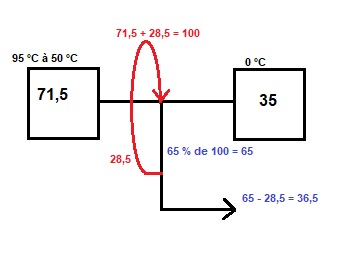
Si le rendement isentropique de la turbine est de 85 %, au sortir de la turbine, nous aurons 65 * 0.85 = 55 dont il faut toujours recycler 28,5 pour pouvoir constamment conserver 100 à l'entrée. Finalement, en tenant compte des pertes, la batterie fournit 55 - 28,5 = 26,5.
Lors de la charge de la batterie avec la pompe à chaleur, nous devons avoir 35 dans le réservoir froid et 71,5 dans le réservoir chaud. La pompe à chaleur doit donc apporter 71,5 - 35 = 36,5 en provenance des éoliennes ou des panneaux solaires. Avec un rendement isentropique de 85 % pour la pompe à chaleur, il faudra charger la batterie avec 36,5 / 0,85 = 43.
L'efficacité aller-retour de la batterie est de 26,5 / 43 = 61 % malgré que nous ayons des réservoirs à basse température.
Nous avons un rendement réel de la turbine de 55 %, ce qui semble trop optimiste, puisque les centrales nucléaires n'ont qu'un rendement de 35 %, mais celles-ci sont refroidies à une température d'environ 60 °C, tandis que dans notre batterie de Carnot, elle est refroidie à 0 °C, ce qui améliore les performances.
J'espère ainsi faire accepter plus facilement cette batterie de Carnot où il n'y qu'une toute petite partie de la machine à très haute température, le reste étant semblable aux boilers que nous avons dans nos maisons.
On pourrait croire que stocker de la chaleur dans de l'eau à 90 °C est moins efficace que la stocker dans du sable à 500 °C. Cependant, l'eau est le composant qui a la plus grande chaleur spécifique parmi les matériaux courants. Si elle est de 1 pour l'eau, elle est de 0,3 pour le sable pour un même volume. Pour un même écart de température, le volume du sable est trois fois plus grand que celui de l'eau. Avec l'eau, nous ne pouvons monter que jusque 100 °C, tandis qu'avec le sable, nous pouvons monter beaucoup plus haut. En conjuguant ces deux aspects, le volume est légèrement réduit avec le sable, mais c'est au prix d'une forte complication de l'installation, alors qu'avec de l'eau chaude, il suffit de plonger deux tuyaux dans l'eau et de pomper. De plus, avec le sable, la différence de température avec l'extérieur est beaucoup plus grande qu'avec l'eau. Cela entraîne des déperditions de chaleur accrues qu'il faudra compenser en agrandissant le réservoir. Finalement, l'eau semble être une solution tout à fait valable.